y=√x функциясы, оның қасиеттері мен графигі 1-сабақ (Б-бөлімі) (Алгебра, 8 сынып, I тоқсан)
Пән: Алгебра
Ұзақ мерзімді жоспар бөлімі: Квадрат түбір және иррационал өрнектер
Сабақ тақырыбы: y=√x функциясы, оның қасиеттері мен графигі 1-сабақ (Б-бөлімі)
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме): 8.4.1.1 y=√x функциясының қасиеттерін білу және оның графигін салу;
8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу.
Сабақ мақсаттары: y=√x функциясының графигін салу;
y=√x функциясының қасиеттерін қолдану;
аргументтің берілген мәндері бойынша y=√x функциясының мәндерін табу;
y=√x функциясының берілген мәні бойынша аргументтің мәнін табу.
Ұйымдастыру кезеңі. Сабақ мақсатын қою.
Мұғалім оқушылармен сәлімдесіп, олардың сабаққа дайындығын тексереді. Мұғалім сабақтың тақырыбы мен оқу мақсаттарын айтады. Оқушылармен бірге сабақ мақсаттары құрастырылып айтылады. Кейін мұғалім бағалау критерийлерін айтып, оқушылардың «жақын даму аймағын» айқындайды, сабақ аяғына қарай күтілетін нәтижелерді айтады.
Қайталау.
Мұғалім оқушылармен талқылау арқылы оларға жаңа материалды меңгеру кезінде қажет болатын негізгі ұғымдарды еске салады: квадрат түбір, иррационал сан, иррационал өрнек.
3. Жаңа тақырыпты түсіндіру.
Мұғалім: Сіз дәрілік шөп өсірумен айналысатын шаруашылық директоры екеніңізді елестетіп көріңізші. Дәрілік дақылдарды аудандары 25 м2, 16 м2, 9 м2, 4 м2, 1 м2 болатын шаршы алаңдарға отырғызу керек. Осы алаңдардың сызықтық өлшемін табыңыз, алаңның өлшемі үздіксіз 0-ден 16 м2-ге дейін өзгереді деп, алаңдардың өлшемдерінің оның аудандарына тәуелділігін график арқылы көрсетіңіз.
Содан кейін мұғалім оқушыларға кері есепті тұжырымдауды ұсынады.
Шаршы алаңдардың 1 м, 2 м, 3 м, 4 м-ге тең болатын сызықтық өлшемдерін біле отырып, алаңдардың аудандарын анықтау қажет. Есептің шартын математикалық модель ретінде жазайық және S-тың а-дан тәуелділігін көрсететін графикті салайық, а 0-ден 4-ке дейін үздіксіз өзгереді деп есептейік.
Одан кейін мұғалім оқушыларға шамалардың атауын у және х-қа алмастыруды, алынған графиктерді бір координаттар жүйесінде құрып, оларды салыстыруды ұсынады.
Мұғалім оқушыларға көмек ретінде келесі сұрақтарды қояды:
Графиктердің бір-біріне қатысты орналасуы туралы не айта аласыз?
Осы функциялардың анықталу облыстарын және мәндер облыстарын салыстырыңыз.
Оқушылардың жауаптарынан кейін мұғалім оларға осы функциялардың графиктерін көрсетеді және оқушылармен бірлесе отырып, y=x^2 (мұндағы х ≥ 0) функциясының графигінің әрбір M(a,b) нүктесіне y=√x функциясының графигінің N(b,a) нүктесі сәйкес келетіні туралы және кері сәйкестік туралы қорытынды шығарады. Сондықтан y=x^2 және y=√x функциялардың графиктері y=x түзуіне қатысты симметриялы болады.
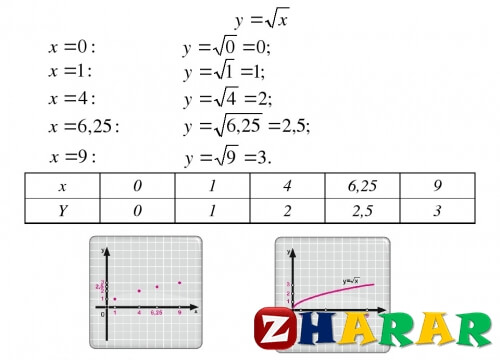
Содан кейін мұғалім квадрат түбірінің функциясының графигі қалай салынатынын түсіндіріп, оқушылармен бірге осы функцияның қасиеттерін анықтайды. Оқушылар функцияның қасиеттерін дәптерге жазады.
4. Өтілген тақырыпты бекіту.
Мұғалім оқушыларға тапсырмаларды жеке орындауды ұсынады. Мұғалім оқушыларға қиындық туған сәтте көмек береді. Оқушылардың типтік қателері бүкіл сыныппен талқыланады.
Оқушылар жұмысты аяқтаған соң, жұптарда өзара бағалау жүргізіледі, сонымен қатар, мұғалім оқушылардың жұмысын белгіленген критерийлерге сәйкес бағалайды.
Бағалау критерийлері:
Оқушы
берілген нүктелерден функциясының графигіне тиісті нүктелерді анықтайды;
аргументтің берілген мәні бойынша функциясының мәнін табады;
функциясының берілген мәндері бойынша аргументтің мәнін табады.......
Ұзақ мерзімді жоспар бөлімі: Квадрат түбір және иррационал өрнектер
Сабақ тақырыбы: y=√x функциясы, оның қасиеттері мен графигі 1-сабақ (Б-бөлімі)
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме): 8.4.1.1 y=√x функциясының қасиеттерін білу және оның графигін салу;
8.4.1.4 аргументтің берілген мәндері бойынша функцияның мәндерін табу және функцияның мәні бойынша аргументтің мәнін табу.
Сабақ мақсаттары: y=√x функциясының графигін салу;
y=√x функциясының қасиеттерін қолдану;
аргументтің берілген мәндері бойынша y=√x функциясының мәндерін табу;
y=√x функциясының берілген мәні бойынша аргументтің мәнін табу.
Ұйымдастыру кезеңі. Сабақ мақсатын қою.
Мұғалім оқушылармен сәлімдесіп, олардың сабаққа дайындығын тексереді. Мұғалім сабақтың тақырыбы мен оқу мақсаттарын айтады. Оқушылармен бірге сабақ мақсаттары құрастырылып айтылады. Кейін мұғалім бағалау критерийлерін айтып, оқушылардың «жақын даму аймағын» айқындайды, сабақ аяғына қарай күтілетін нәтижелерді айтады.
Қайталау.
Мұғалім оқушылармен талқылау арқылы оларға жаңа материалды меңгеру кезінде қажет болатын негізгі ұғымдарды еске салады: квадрат түбір, иррационал сан, иррационал өрнек.
3. Жаңа тақырыпты түсіндіру.
Мұғалім: Сіз дәрілік шөп өсірумен айналысатын шаруашылық директоры екеніңізді елестетіп көріңізші. Дәрілік дақылдарды аудандары 25 м2, 16 м2, 9 м2, 4 м2, 1 м2 болатын шаршы алаңдарға отырғызу керек. Осы алаңдардың сызықтық өлшемін табыңыз, алаңның өлшемі үздіксіз 0-ден 16 м2-ге дейін өзгереді деп, алаңдардың өлшемдерінің оның аудандарына тәуелділігін график арқылы көрсетіңіз.
Содан кейін мұғалім оқушыларға кері есепті тұжырымдауды ұсынады.
Шаршы алаңдардың 1 м, 2 м, 3 м, 4 м-ге тең болатын сызықтық өлшемдерін біле отырып, алаңдардың аудандарын анықтау қажет. Есептің шартын математикалық модель ретінде жазайық және S-тың а-дан тәуелділігін көрсететін графикті салайық, а 0-ден 4-ке дейін үздіксіз өзгереді деп есептейік.
Одан кейін мұғалім оқушыларға шамалардың атауын у және х-қа алмастыруды, алынған графиктерді бір координаттар жүйесінде құрып, оларды салыстыруды ұсынады.
Мұғалім оқушыларға көмек ретінде келесі сұрақтарды қояды:
Графиктердің бір-біріне қатысты орналасуы туралы не айта аласыз?
Осы функциялардың анықталу облыстарын және мәндер облыстарын салыстырыңыз.
Оқушылардың жауаптарынан кейін мұғалім оларға осы функциялардың графиктерін көрсетеді және оқушылармен бірлесе отырып, y=x^2 (мұндағы х ≥ 0) функциясының графигінің әрбір M(a,b) нүктесіне y=√x функциясының графигінің N(b,a) нүктесі сәйкес келетіні туралы және кері сәйкестік туралы қорытынды шығарады. Сондықтан y=x^2 және y=√x функциялардың графиктері y=x түзуіне қатысты симметриялы болады.
Содан кейін мұғалім квадрат түбірінің функциясының графигі қалай салынатынын түсіндіріп, оқушылармен бірге осы функцияның қасиеттерін анықтайды. Оқушылар функцияның қасиеттерін дәптерге жазады.
4. Өтілген тақырыпты бекіту.
Мұғалім оқушыларға тапсырмаларды жеке орындауды ұсынады. Мұғалім оқушыларға қиындық туған сәтте көмек береді. Оқушылардың типтік қателері бүкіл сыныппен талқыланады.
Оқушылар жұмысты аяқтаған соң, жұптарда өзара бағалау жүргізіледі, сонымен қатар, мұғалім оқушылардың жұмысын белгіленген критерийлерге сәйкес бағалайды.
Бағалау критерийлері:
Оқушы
берілген нүктелерден функциясының графигіне тиісті нүктелерді анықтайды;
аргументтің берілген мәні бойынша функциясының мәнін табады;
функциясының берілген мәндері бойынша аргументтің мәнін табады.......
Толық нұсқасын 30 секундтан кейін жүктей аласыз!!!
Әлеуметтік желілерде бөлісіңіз:
Facebook | VK | WhatsApp | Telegram | Twitter
Қарап көріңіз 👇
Пайдалы сілтемелер:
» Туған күнге 99 тілектер жинағы: өз сөзімен, қысқаша, қарапайым туған күнге тілек
» Абай Құнанбаев барлық өлеңдер жинағын жүктеу, оқу
» Дастархан батасы: дастарханға бата беру, ас қайыру
Соңғы жаңалықтар:
» Грузия қазақстандықтарға білім грантын бөлді
» Қазақстандықтар шетелге қай мезгілде жиірек шығады
» Freedom bank-те керемет акция! 1000 ₸ кэшбек сыйлайды

